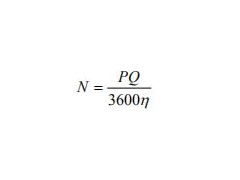吳文忠

（西安科技大學，陜西西安   710054）

摘   要：煙氣壓力和溫度是高層住宅廚房豎向集中排煙系統的基本參數。住戶油煙機開啟工況服從泊松過程，驅動豎井內煙氣壓力和溫度變化，因此本研究應用守恒定律和泊松過程知識，首先分析隨開啟工況變化的排煙中性層高度、豎井出口處煙氣壓力分布函數，接著分析隨開啟工況變化的豎井出口處煙氣溫度分布函數。由這二類分布函數，應用隨機分析方法進一步計算任意開啟工況下豎井出口處煙氣壓力和溫度。這二類基本參數是排煙系統優化排煙效果和回收利用排煙熱量的基礎。

關鍵詞：高層住宅；廚房；集中排煙系統；壓力；煙氣溫度；泊松過程

0   引言

廚房排煙中含有CO、CO₂、塵埃等有害物質，為了保證廚房清潔，高層住宅設計豎向集中排風系統。龔勝強等^[1]模擬了給定開啟工況時豎井內靜壓分布規律，底層壓力最大，頂層壓力最小，開啟率越大，豎井內靜壓值越大，而且靜壓值受開啟不均勻特性影響。

由于豎井內靜壓分布總體上自上而下逐漸增大，排煙量則自上而下逐漸減小，低層用戶排煙量很低，底層用戶排煙量最小。因此高軍等^[2]在單純用戶動力的基礎上，在豎井出口設置排煙風機，和用戶抽油煙機構成復合動力系統，獲得高效率的排煙效果。

根據我國住宅居住調查：高層住宅樓內同一排風道系統的吸油煙機同時開機率一般在30%~60%之間，多數情況為20%~55%的開機率。

在給定開機率時，排煙參數表現出不均勻性質，有不同的描述參數：龔勝強等[1]定義排煙路徑長度描述開啟不均勻特性；高軍等^[2]采用靜壓方差，皮李^[3]采用排氣系統不均勻率。

在自然排煙方式下，由于煙囪效應，建筑室內，樓梯間、電梯間、室內和豎井內靜壓分布存在中性層，向伊依等[3]通過對學生公寓樓和綜合樓測試表明了中性層高度和各層靜壓分布。豎井出口處壓力隨中性層高度變化，進而影響排煙效果。在排煙系統中，中性層高度影響豎井內靜壓分布，也影響出口處排煙量。

廚房排煙是燃料燃燒產物，溫度高于環境溫度，應用熱回收節能技術手段，可以節約能源，起到減排的作用，有著積極的社會效益和環境效益^[4-5]。

張鑫等^[5]為了設計桌面燒烤排氣罩，實測燒烤盤加熱面溫度在180~380℃，與周圍空氣最大溫度差360℃。廚房排煙在豎井出口處溫度是設計熱回收節能措施的參數。

住戶開啟排煙是隨機事件，服從二項式分布，開啟排煙機的累計數量是一個泊松過程。受該過程驅使，集中排煙系統豎井內壓力和溫度分布呈現隨機變化特性，因此本研究應用守恒定律和泊松過程知識[7-9]，首先分析隨開啟工況變化的排煙中性層高度、豎井出口處煙氣壓力分布函數、豎井出口處煙氣溫度分布函數。由這二類分布函數，應用微分幾何知識^[10-12]和隨機分析方法^[13-14]進一步計算任意開啟工況下豎井出口處煙氣壓力和溫度。這二類基本參數是排煙系統優化排煙效果和回收利用排煙熱量的基礎。

1   排煙工況隨機特性

假設某高層住宅有N個住戶，每戶使用相同抽油煙機，排煙量均為m，排風扇壓力均為p，屋頂風機壓力pceiling，誘導豎井出口處排煙速度v_n。

1.1   開機工況服從泊松分布

考察同一排風道系統的吸油煙機同時開機率：對于一個用戶，開機工況有二個：“開機”和“不開機”，服從概率約為1/24（每天開機1h）的二項分布，對于N個住戶，開機工況也是服從二項分布，且當住戶數充分大而每戶開機概率很小（小于0.1）時，該分布近似地表示為λ=N/24
的齊次泊松過程分布函數：

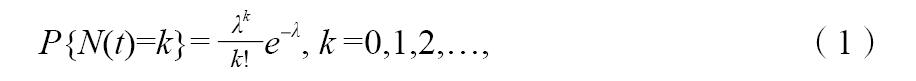
這也是開機率為N(t)/N的概率分布函數。

1.2   排煙工況模擬

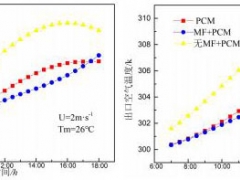
已知排煙工況服從泊松過程，設定住戶數和考察時間，可以應用Matlab軟件對開啟過程進行隨機模擬。圖1是λ=2的開啟過程在50s時間內的變化情況。

圖1   λ=2的開啟過程在50s時間內的變化情況

2   排煙豎井內煙氣中性層高度分布函數

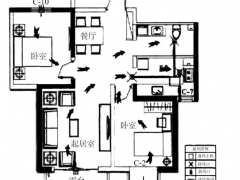
高層建筑廚房集中排煙系統，采用變截面或等截面排煙豎井形式，其中等截面排煙豎井形式應用最廣，如圖2。選取豎井為控制體積。

圖2   高層建筑廚房等截面豎井集中排煙系統示意圖

給定開啟工況N(t)=k。選取豎井不同截面，考察排煙機械能守恒。假設用戶風機壓力僅提供分散排煙動能。下部不開口，僅在豎井出口處開口，出口處沒有流動時，中性層在出口處，豎井內部任意高度處靜壓是負值，即：

當豎井出口處附加屋頂風機時，假設用戶風機壓力全部轉化為煙氣動能，則豎井內部中性層不變，仍維持在豎井出口處，即：

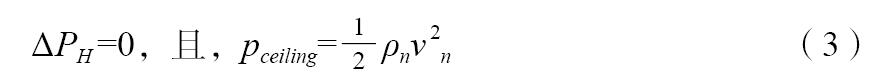
于是在出口處排出煙氣量為:

更一般地，當采用混合動力排煙方式時，用戶風機、屋頂風機壓力均貢獻豎井內靜壓。假設豎井底部內外靜壓差維持：

則豎井出口處靜壓差：

忽略不同高度處動能差，則豎井內任意高度處靜壓差：

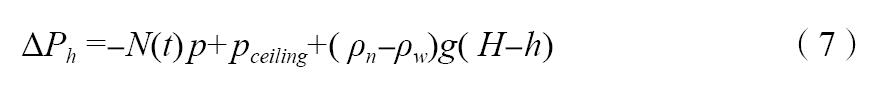
在上式中令ΔPh =0，得到中性層高度：

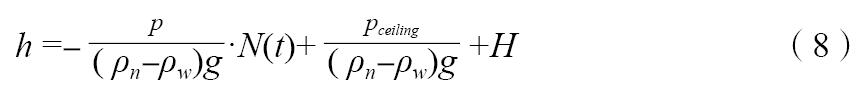
顯然，當采用分散動力排煙方式，即pceiling=0時，給定高度h處壓力ΔPh的絕對值隨開機數量增大而增大；當采用混合動力排煙方式，并保持給定高度h處壓力ΔPh不變時，屋頂風機壓力pceiling隨開機數量增大而增大。

由上式和開機工況分布函數式（1），并記：

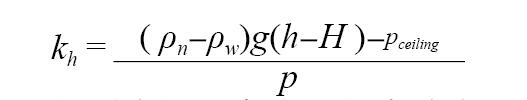
得到中性層高度的概率分布函數為：

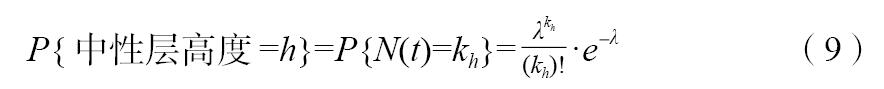
3   豎井出口處煙氣參數分布函數

對于同一排風道系統，主要考察豎井出口處參數。該處靜壓已經由式（6）得到，而且因此得到豎井出口處排煙量：

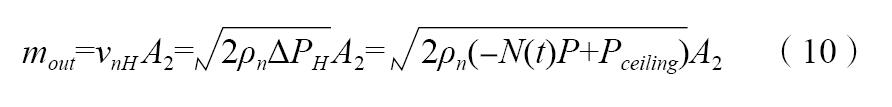
3.1   煙氣參數分布函數

在豎井出口處，煙氣溫度由局部理想氣體狀態方程和式（6）得到：

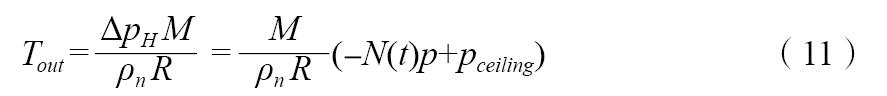
式中：M是煙氣摩爾質量，R是理想氣體狀態常數。

由上式和開機工況分布函數式（1），并記：

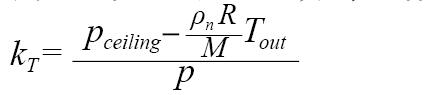
得到出口處排煙溫度的概率分布函數為：

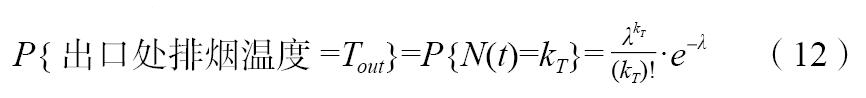
由式（6）和開機工況分布函數式（1），并記：

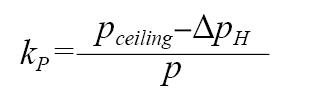
得到出口處排煙溫度的概率分布函數為：

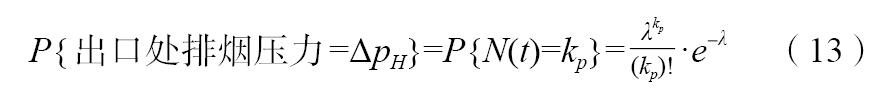
3.2   煙氣參數不均勻性質

前文已經得到出口處煙氣參數概率分布函數。如果給定開機工況N(t)=k，這些開啟樓層位于不同的高度，排煙路徑總長度不同，會加劇煙氣參數不均勻。已知開機工況服從泊松過程，給定開機工況下排煙路徑長度也是隨機變量，假設這二個序列相互獨立，應用排煙路徑總長度變化過程描述排煙參數不均勻性，則該過程是典型的復合泊松過程：

它的數學期望為：

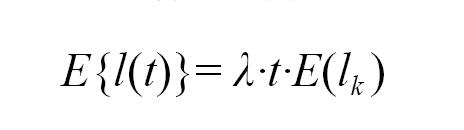
方差為：

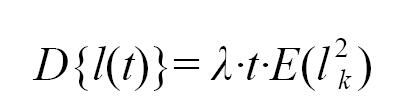
則該不均勻過程的極限分布函數近似為期望為λ·t·E(lk )，方差為λ·t·E(l2k )的正態分布函數：

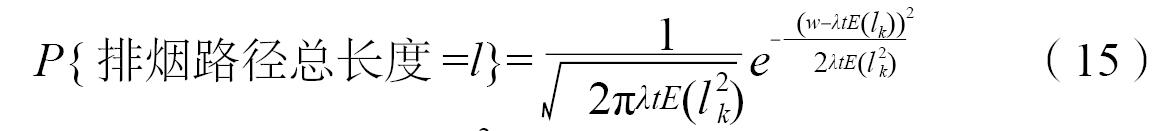
圖3是E(lk )=0，λ·E(l2k )=1，t=1s時間內排煙參數不均勻過程模擬情況。

圖3   排煙參數不均勻過程模擬

因為給定開機工況時，不同的排煙路徑長度也會影響煙氣參數，因此根據式（15）修正排煙參數分布函數式（12）和（13）為：

式中：α和β是常數，且α+β=1，最簡單取值情況為α=β=1/2。

4   任意開啟工況下豎井出口處排煙參數

已知開啟工況服從泊松過程，排煙參數不均勻性質近似服從正態分布，按照前述結果可計算豎井出口處排煙參數均值。更細致地，應計算在隨機開啟工況和不均勻性質條件下排煙參數的條件數學期望。

4.1   排煙條件

開啟工況服從泊松分布，分布函數按式（1）；不均勻性質近似服從正態分布，分布函數按式（15）。排煙系統處于地面上重力環境中，存在牛頓引力勢：

記RN空間內單位球面積為a(N)，有：a(2)=2π，a(3)=4π，…，則牛頓引力勢核為：

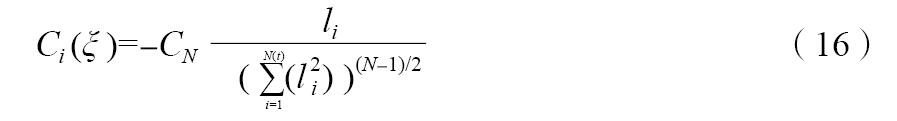
式中：CN = 2(N-2)/a(N ), N > 2。

4.2   排煙參數計算

考察在上述條件下計算豎井出口處排煙參數，則首先需要計算該處排煙參數條件數學期望。記出口處壓力和溫度的張量仍為[8-10]。由隨機分析理論[11-12]得到任意開啟工況下出口處煙氣壓力的條件數學期望為：

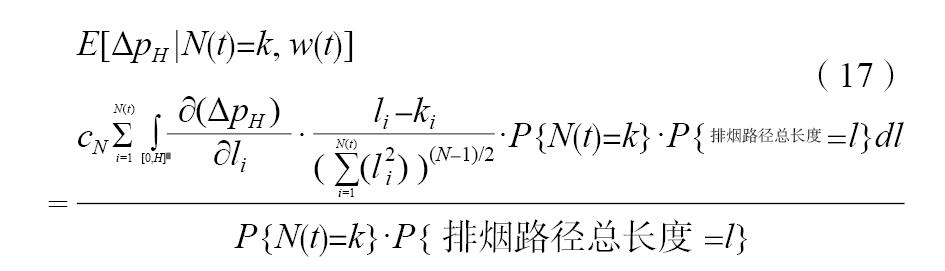
由此得到出口處煙氣壓力為：

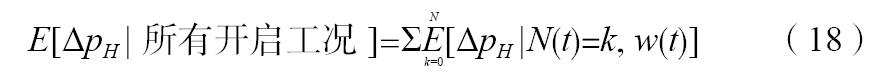
在上式中替換ΔpH為Tout，得到出口處煙氣溫度。顯然，如果不考慮排煙參數的隨機特性，即令上式中概率分布函數均等于1，上式就是給定開機工況N(t)=k時豎井出口處煙氣壓力式（6）和溫度（11）。

5   結論

煙氣壓力和溫度是高層住宅廚房豎向集中排煙系統的基本參數，也是排煙系統優化排煙效果和回收利用排煙熱量的基礎。這二個參數受住戶油煙機開啟工況的隨機特性驅動。

排煙環境中，開啟工況服從泊松過程，排煙參數不均勻度以正態分布為極限分布，因此本研究首先推導了開啟工況和排煙參數不均勻度概率分布函數，接著應用機械能守恒定律，推導了隨開啟工況隨機特性驅動的排煙中性層高度、豎井出口處煙氣壓力和溫度概率分布函數。為了分析在隨機開啟工況條件下豎井出口處煙氣參數，應用隨機分析方法和這二類分布函數，進一步推導了任意開啟工況下該處煙氣壓力和溫度的計算公式，它們包含了給定開機工況時豎井出口處煙氣參數計算方法。

參考文獻

[1] 龔勝強，劉勇，熊健，王振飛，張鈺巧. 高層住宅廚房集中排煙系統特性研究 [J]．建筑技術開發，2016增刊：173–178．

[2] 高軍，丁希暉，陳磊，吳利. 高層住宅廚房復合動力變排風量系統及其特性計算 [C].2016年第二十屆全國暖通空調制冷學術年會論文集，目次：138．

[3] 皮李. 高層建筑等截面多動力源排風道流動特性計算與模擬分析 [D]. 西安：西安建筑科技大學，2104.

[4] 向伊依，潘嵩，張健宸，林瑤，程作. 北方地區高層建筑在“煙囪效應”作用下的不同豎井區域壓差分布特性及節能策略 [J]．建筑技術開發，2016,vol.43(10):41–45．

[5] 劉云祥. 排風熱回收系統應用的探討 [J]．暖通空調 ＨＶ＆ＡＣ,2012vol.42(7):72–77.

[6] 張鑫，劉紹忠. 淺談桌面燒烤排氣罩設計 [C].2016年第二十屆全國暖通空調制冷學術年會資料集,目次：064．

[7] WU Wen-zhong. Stochastic prediction and control to methane in coalmine [J]. Journal of Coal Science & Engineering (China), 2011,vol.17(3):321–325.

[8] 魏艷華,王丙參,宋立新.復合泊松過程性質及其應用 [J].宜賓學院學報,2009,9 (12):45–48.

[9] 孫天晴.基于復合泊松過程戰略石油儲備天數的概率模型及其應用 [J].數理統計與管理,2007,26 (5):12–14.

[10] 馬力. 簡明微分幾何 [M]. 北京：清華大學出版社，2004.

[11] 劉連壽，鄭小平. 張量分析 [M]. 北京：科學出版社，2008.

[12] 高麗敏，李開泰，劉波，蘇劍. 積分守恒型N-S方程通用形式及其在數值模擬中的應用 [J]. 計算物理CHINESE JOURNAL OF COMPUTATIONAL PHYSICS，2008 vol.25(2):172–178.

[13] Paul Malliavin. Stochastic Analysis [M]. Springer-Verlag, berlin, 2006.

[14] Paul Malliavin, Anton Thalmaier. Stochastic Calculus of Variations in Mathematical Finance [M]. Springer-Verlag, berlin, 2006.

注：本文收錄于《建筑環境與能源》2017年5月刊總第5期《2017全國通風技術年會論文集》中。
版權歸論文作者所有，任何形式轉載請聯系作者。