上海理工大學(xué)環(huán)境與建筑學(xué)院  胡浩 王海東  楊昕琦

       【摘  要】分層空調(diào)系統(tǒng)以其顯著的節(jié)能潛力廣泛應(yīng)用于大空間建筑，其內(nèi)部的熱量遷移對負(fù)荷和能耗產(chǎn)生顯著影響，因而獲得廣泛關(guān)注。為了準(zhǔn)確預(yù)測大空間建筑的室內(nèi)熱環(huán)境和負(fù)荷特性，本文利用實驗與CFD方法，研究了柱狀下送風(fēng)和側(cè)壁噴口送風(fēng)兩種典型氣流組織下，非空調(diào)區(qū)和空調(diào)區(qū)之間的對流熱轉(zhuǎn)移。在縮尺實驗室中進(jìn)行實驗測試，以對CFD數(shù)值模型進(jìn)行精確度驗證。基于相似理論，將縮尺工況拓展到全尺寸工況模擬，討論了兩種送風(fēng)系統(tǒng)下區(qū)域間換熱情況，為降低分層空調(diào)能耗提供理論指導(dǎo)。結(jié)果表明，對于柱狀下送風(fēng)系統(tǒng)，溫度梯度引起的熱傳導(dǎo)起主要作用。而在側(cè)壁噴口送風(fēng)系統(tǒng)中，溫度梯度引起的熱傳導(dǎo)和氣流流動引起的換熱量均不容忽視。送風(fēng)方式、區(qū)域劃分以及局部湍流強度對區(qū)域間換熱系數(shù)Cb均有影響。

       【關(guān)鍵詞】大空間建筑；分層空調(diào)；CFD；對流熱轉(zhuǎn)移；區(qū)域間換熱系數(shù)

       【基金項目】國家自然科學(xué)基金（51508326）

0 引言

       大空間建筑中，人員活動區(qū)域的高度遠(yuǎn)低于建筑高度。為了減少冷量的消耗，多采用分層空調(diào)系統(tǒng)對室內(nèi)空氣進(jìn)行調(diào)節(jié)^[1]。分層空調(diào)是指對大空間建筑下部區(qū)域進(jìn)行空氣調(diào)節(jié)，而對上部區(qū)域不進(jìn)行空氣調(diào)節(jié)的空調(diào)系統(tǒng)^[2]。與全室空調(diào)相比，分層空調(diào)可顯著減少室內(nèi)冷負(fù)荷、降低系統(tǒng)運行成本^[3]。準(zhǔn)確計算分層空調(diào)冷負(fù)荷在設(shè)備選型和建筑節(jié)能方面起著至關(guān)重要的作用。大空間建筑由于其內(nèi)部空間高、體積大的特點，致使垂直方向上熱分層現(xiàn)象十分顯著，大部分熱量聚集在屋頂，并通過輻射和對流的方式向空調(diào)區(qū)轉(zhuǎn)移，增加空調(diào)區(qū)的冷負(fù)荷。

       非空調(diào)區(qū)向空調(diào)區(qū)轉(zhuǎn)移的對流換熱量是分層空調(diào)負(fù)荷計算的關(guān)鍵，從微觀上看這部分熱量包括分層面上下空氣層間由于氣流流動產(chǎn)生的換熱量和溫度梯度引起的導(dǎo)熱量。其中，氣流換熱量可以通過分層面處的氣流質(zhì)量流量計算得到，而溫差換熱量不容易計算得到。Togari等^[4]提出了一種溫度基準(zhǔn)區(qū)域模型來預(yù)測大空間建筑能耗和室內(nèi)熱環(huán)境，并實驗得到傳熱系數(shù)Cb=2.3W/(m²·℃)來估算大空間建筑分層面上的溫差導(dǎo)熱量。Cb被定義為區(qū)域溫差換熱系數(shù)，是指單位面積單位溫差下通過空氣層的熱交換量，不包括空氣質(zhì)量交換產(chǎn)生的熱交換量。然而經(jīng)驗系數(shù)Cb并不能夠完全適用于所有的大空間建筑分層面上熱量計算。高軍等^[5]從理論上闡明Cb數(shù)學(xué)解析公式，并把該系數(shù)與空氣湍流狀況相關(guān)聯(lián)。氣流換熱量與溫差導(dǎo)熱量的成因不同，這意味著對于不同的空調(diào)系統(tǒng)，兩者在分層面上對流轉(zhuǎn)移熱中的占比有所不同。

       本文旨在研究大空間建筑分層空調(diào)系統(tǒng)區(qū)域間換熱特性，采用實驗與CFD方法，針對大空間建筑兩種典型的送風(fēng)系統(tǒng)：柱狀下送風(fēng)系統(tǒng)和側(cè)壁噴口送風(fēng)系統(tǒng)，討論了屋頂無排風(fēng)情況下，兩種送風(fēng)系統(tǒng)的室內(nèi)溫度分布情況以及冷負(fù)荷預(yù)測。縮尺模型實驗旨在保證 CFD模擬的準(zhǔn)確性，將驗證過的縮尺數(shù)值模型通過相似理論拓展到全尺寸工況模擬，以反映實際大空間建筑室內(nèi)熱環(huán)境。另一方面，本文通過全尺模擬結(jié)果著重分析了兩種系統(tǒng)下Cb的分布情況和產(chǎn)生差異的原因，為分層空調(diào)負(fù)荷計算的研究提供理論指導(dǎo)。此外，本文對比了兩種系統(tǒng)中由于氣流流動和溫差導(dǎo)熱產(chǎn)生的熱量占比情況，為減少對流轉(zhuǎn)移熱提供解決方案。

1 方法

       1.1 實驗

       為了研究大空間建筑兩種典型分層空調(diào)系統(tǒng)下的區(qū)域間換熱特性，采用了一個帶有柱狀下送風(fēng)口和側(cè)壁噴口的縮尺實驗室。該縮尺模型實驗室是基于真實的高大空間建筑建造的，模型與原型的幾何比例為1：4。實驗室的尺寸為3.5×4.9×1.5 ~ 2.2 m，如圖1所示。本實驗為屋頂無排風(fēng)工況，熱源設(shè)置在1.6m。縮尺模型實驗室墻和屋頂貼有均勻發(fā)熱的熱電膜，模擬穩(wěn)態(tài)條件下的圍護(hù)結(jié)構(gòu)得熱，地面敷設(shè)100mm的保溫層降低熱量散失。

       室內(nèi)中心位置布置一條垂直溫度測線，空氣溫度采用Tsic506溫度測點（測量范圍：-10℃~+60℃，分辨率：0.01℃）進(jìn)行測試，測點共22個，間距為100mm。送回風(fēng)溫度和速度均采用SWA-300熱線風(fēng)速儀（測量范圍：0.1~30m/s，分辨率：0.1 m/s）在送風(fēng)主管處進(jìn)行測試，經(jīng)過圓管內(nèi)速度修正后可得到實驗的送風(fēng)量和平均送風(fēng)溫度。屋頂和壁面熱流密度采用JTNT-A建通熱流密度計（測量范圍：0~2000W/m²，分辨率：0.1 W/m²）和HFP01熱流密度計（測量范圍：-2000~2000W/m²，分辨率：0.1 W/m2）進(jìn)行測量。

（a） 柱狀下送風(fēng)系統(tǒng)                    （b） 側(cè)壁噴口送風(fēng)系統(tǒng)
圖1 實驗系統(tǒng)示意圖

       1.2 相似理論

       對室內(nèi)熱環(huán)境來說，溫度場相似是模型與原型需要達(dá)到的主要目的。通常將雷諾數(shù)(Re數(shù))和阿基米德數(shù)(Ar數(shù))作為獲得原型和模型相似的準(zhǔn)則數(shù)。當(dāng)空氣作為介質(zhì)流體時，原型與模型的Re數(shù)和Ar數(shù)不能同時達(dá)到相同^[6]。解決這一問題最常見的方法是將Ar數(shù)作為主要準(zhǔn)則數(shù)，使其在原型和模型中相等，Re 數(shù)則只需保證進(jìn)入自模區(qū)。本研究所有案例的雷諾數(shù)均遠(yuǎn)大于臨界雷諾數(shù)2300^[7]，因此僅控制模型和原型的Ar數(shù)相等。

                                       (1)

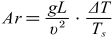                                (2)

       式中：ρ為流體密度（kg/m³）；υ為流體流動速度（m/s）；L為特征長度（m）；μ為流體動力粘度（N·s/m²）；g為重力加速度（m/s²）；ΔT為送風(fēng)氣流與室內(nèi)空氣的溫差（℃）；Ts為送風(fēng)溫度（℃）。

       考慮到室內(nèi)空氣的熱交換，根據(jù)熱量傳遞能量方程：

       Q=ρυC_pFΔT                      (3)

       式中：C_p為空氣定壓比熱容（J/(kg·℃)）；F為送風(fēng)口面積（m²）。

       將其帶入到Ar數(shù)中，可以引出熱量阿基米德數(shù)ArQ：     

                                    (4)

       通過相似條件的轉(zhuǎn)換，式（2）和（4）即可分別表述為：

                                     (5)

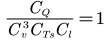                               (6)

       將送風(fēng)溫度比例尺C_Ts和溫差比例尺CΔT都定為1，相應(yīng)的其他比例尺如下表1所示：

表1 各個參數(shù)比例尺匯總

       1.3 CFD模擬研究本文采用CF

       D模擬軟件PHOENICS進(jìn)行數(shù)值計算。根據(jù)實驗室尺寸，建立了CFD幾何模型，房間送回風(fēng)口面積和實驗室保持一致。微分方程組的離散采用控制容積法，壓力-速度耦合采用SIMPLE算法，其中湍流模型采用標(biāo)準(zhǔn)k-ω模型，輻射模型采用IMMERSOL模型。

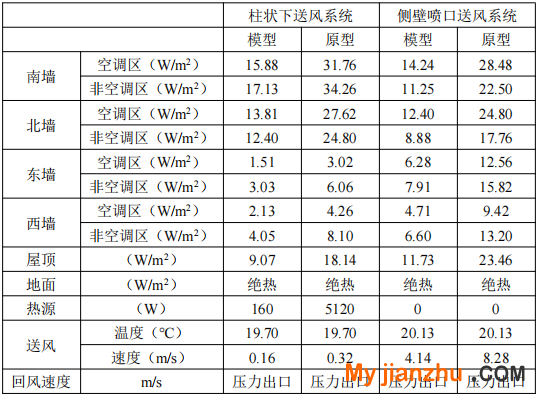
       本文研究穩(wěn)態(tài)工況，實驗和數(shù)值模擬壁面的熱量均為恒定值。在縮尺數(shù)值模型中，根據(jù)實驗測得數(shù)據(jù)設(shè)置墻和屋頂?shù)臒崃髅芏戎担粚τ谌吣Ｐ停溥吔鐥l件是根據(jù)縮尺工況條件以及相似比例尺確定。墻、屋頂、地面發(fā)射率取為0.93。送風(fēng)口采用速度邊界條件，回風(fēng)口采用壓力出口，邊界條件如表2所示。

表2 數(shù)值模擬邊界條件設(shè)置

2  CFD結(jié)果驗證

       2.1 垂直溫度分布

       如圖2（a）、3（a）所示，在兩種送風(fēng)系統(tǒng)縮尺模型下，實驗和數(shù)值模擬得到中心測線溫度分布基本一致，說明數(shù)值模擬結(jié)果可以較好的反映室內(nèi)熱環(huán)境。將驗證過的縮尺模型按幾何比例尺Cl=4放大成原型進(jìn)行數(shù)值計算，得到全尺模型的中心線溫度分布，如圖2（b）、3（b）所示，可以看出原型與模型的室內(nèi)熱環(huán)境相似。

       2.2 縮尺模型冷負(fù)荷驗證

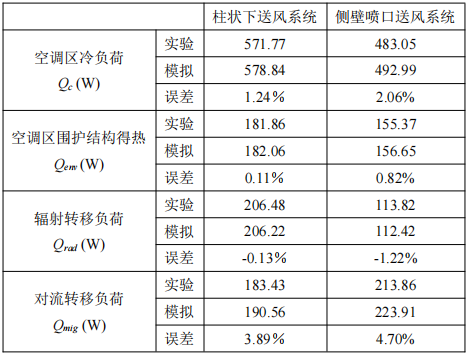
       大空間建筑中，非空調(diào)區(qū)到空調(diào)區(qū)的熱遷移是評價冷負(fù)荷的關(guān)鍵。在高大空間分層空調(diào)的分層界面上，存在質(zhì)量和熱量交換，這部分的熱量交換即為非空調(diào)區(qū)向空調(diào)區(qū)的對流熱轉(zhuǎn)移負(fù)荷。由于不考慮排風(fēng)的影響，從系統(tǒng)能量平衡的角度，空調(diào)區(qū)的冷負(fù)荷Qc可由公式（7）計算。

                                   (7)

       式中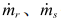：分別為回風(fēng)量、送風(fēng)量（kg/s）；t_r、t_s分別為回風(fēng)溫度、送風(fēng)溫度（℃）。

圖2 兩種尺度下柱狀下送風(fēng)系統(tǒng)中心測線垂直溫度分布

圖3 兩種尺度下側(cè)壁噴口送風(fēng)系統(tǒng)中心測線垂直溫度分布

       由于模型不考慮各個壁面的蓄熱，因此可認(rèn)為各個壁面向外輻射熱流量等于輻射轉(zhuǎn)移負(fù)荷。采用文獻(xiàn)[8]中的方法來計算非空調(diào)區(qū)各個壁面向空調(diào)區(qū)輻射熱量之和，即輻射轉(zhuǎn)移熱Q_rad；根據(jù)熱量平衡關(guān)系，非空調(diào)區(qū)向空調(diào)區(qū)的對流轉(zhuǎn)移熱Q_mig可由公式（8）得到。

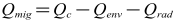                                  (8)

       由表3可以看出，兩種送風(fēng)系統(tǒng)縮尺模型下，實驗和CFD數(shù)值模擬得到的空調(diào)區(qū)冷負(fù)荷之間的誤差分別為1.24%、2.06%。因此CFD模擬得到冷負(fù)荷能較好的反映實驗結(jié)果，將驗證后的數(shù)值模型拓展到全尺寸工況。

3 結(jié)果分析

       3.1 對流轉(zhuǎn)移熱分析

       從微觀上看，分層界面上的對流轉(zhuǎn)移熱Q_mig一部分是由于氣體質(zhì)量流量引起的氣流換熱量Q_conv，另一部分是由于溫差引起的導(dǎo)熱量Q_cond。因此，Q_mig可由公式（9）計算。

                                    (9)

       總質(zhì)量流量引起的氣流換熱量Q_conv可由公式（10）計算得到。

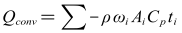                               (10)

       式中：ω_i為節(jié)點垂直速度分量（m/s）;A_i為第i個網(wǎng)格的面積（m²）;t_i為第i個網(wǎng)格的空氣溫度（℃）。

表3 基于縮尺模型的實驗與CFD模擬得到的冷負(fù)荷對比

 

       由于受到湍流的影響，氣體間的導(dǎo)熱有別于固體間的導(dǎo)熱，除了氣體本身的導(dǎo)熱系數(shù)外，還與氣體的湍流強度有關(guān)。溫度梯度引起的熱傳導(dǎo)Q_cond可由式（11）計算得到。

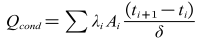                          (11)

       式中：λ_i為第i個節(jié)點空氣的湍流熱導(dǎo)率（W/(m·℃)）；δ為網(wǎng)格厚度（m）。

表4 基于兩種尺度數(shù)值模擬得到的對流轉(zhuǎn)移熱對比

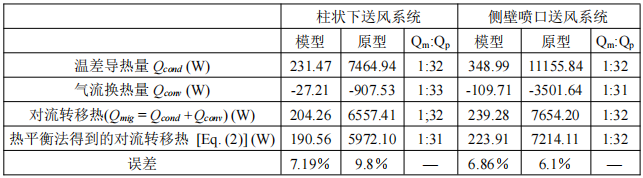
       根據(jù)兩種尺度的數(shù)值模擬結(jié)果，表4說明了CFD方法的可靠性，并驗證了相似比的正確性。其結(jié)果表明，在柱狀下送風(fēng)系統(tǒng)中，對流轉(zhuǎn)移熱中由溫差引起的熱傳導(dǎo)起主導(dǎo)作用。而在側(cè)壁噴口送風(fēng)系統(tǒng)中，氣流流動引起的換熱和溫差引起的熱傳導(dǎo)均不容忽視。

       3.2  區(qū)域間換熱系數(shù)

       3.2.1 兩區(qū)域劃分下的結(jié)果對比

       區(qū)域溫差換熱系數(shù)Cb是指單位面積單位溫差下通過空氣層的熱交換量，表征區(qū)域間溫差引起的熱轉(zhuǎn)移能力的大小，與空氣質(zhì)量流動產(chǎn)生的熱交換量無關(guān)。如圖4所示，提出了一種基于網(wǎng)格節(jié)點的數(shù)值分析方法來求解區(qū)域溫差換熱系數(shù)。Cb對預(yù)測大空間建筑室內(nèi)熱環(huán)境和負(fù)荷具有重要的意義。

                          (12)

       式中：A為兩個區(qū)域相互接觸面積（m²）;t_upzone、t_downzone分別為上部區(qū)域、下部區(qū)域的特征溫度（℃）。

圖4 數(shù)值法求解Cb網(wǎng)格節(jié)點示意圖

       基于全尺模型模擬結(jié)果，在柱狀下送風(fēng)系統(tǒng)Z=4.5m處，劃分為上部非空調(diào)區(qū)和下部空調(diào)區(qū)；而對于噴口送風(fēng)系統(tǒng)中，分層面選取在Z=4.1m。根據(jù)公式（12）計算得到分層面處的區(qū)域間換熱系數(shù)值。

表5 兩種送風(fēng)系統(tǒng)二區(qū)域劃分下得到的區(qū)域間換熱系數(shù)

       由表5可知，原型的Cb值約為縮尺工況下的2倍。在兩種送風(fēng)系統(tǒng)中，Cb值的差異主要因為噴口射流在上下界面之間產(chǎn)生更強得湍流，這一點能從湍流導(dǎo)熱系數(shù)的數(shù)值上體現(xiàn)。這表明，氣流組織形式對層間換熱系數(shù)的取值有一定影響。

       3.2.2 四區(qū)域劃分下的結(jié)果對比

       由于區(qū)域劃分方式影響著區(qū)域的特征溫度，對于不同區(qū)域劃分時，分界面上Cb值存在差異。考慮到送、回風(fēng)口和坡屋頂?shù)挠绊懀谌吖r二區(qū)域劃分下，進(jìn)一步在Z=2m、Z=6m高度將整個空間劃分為四個區(qū)域。由式（12）計算不同截面溫差換熱系數(shù)，其結(jié)果列于表6，Cb分布云圖如圖5、圖6所示。

       在四區(qū)域的劃分中，不同高度的分界面上，溫差換熱系數(shù)Cb的值存在較大差距。在柱狀下送風(fēng)系統(tǒng)中，由于送風(fēng)口空氣流動和回風(fēng)口抽吸的影響，使得空調(diào)區(qū)和分層面處的氣流擾動較大，區(qū)域間換熱系數(shù)較大；在非空調(diào)區(qū)，氣流相對穩(wěn)定，Cb值較小。而對于側(cè)壁噴口送風(fēng)系統(tǒng)，在Z=2m分界面處,回風(fēng)口的抽吸作用使得氣流流動較強，空氣的湍流導(dǎo)熱率較大，使得Cb值較大；在分層面處，噴口附近湍流波動劇烈，遠(yuǎn)離送風(fēng)口的氣流相對穩(wěn)定，此界面處的Cb值為80.11 W/(m2·℃)；非空調(diào)區(qū)雖然垂直溫度梯度較大，但沒有很強烈的氣流，因此Cb較小。

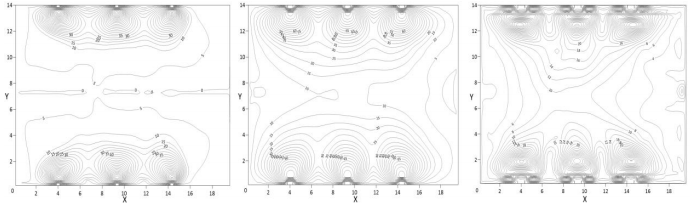
圖5 柱狀下送風(fēng)系統(tǒng)Cb在z=2m、z=4.5m、z=6m高度處的分布云圖

圖6 側(cè)壁噴口送風(fēng)系統(tǒng)Cb在z=2m、z=4.1m、z=6m高度處的分布云圖
表6 不同分界面處溫差換熱系數(shù)Cb W/(m²·?C)和湍流導(dǎo)熱系數(shù)W/(m·?C)值

       在實際工程中，應(yīng)盡量減弱非空調(diào)區(qū)和空調(diào)區(qū)之間的空氣擾動。對于噴口送風(fēng)系統(tǒng)，在保證系統(tǒng)冷量和空調(diào)區(qū)舒適性的前提下，可以采取風(fēng)速較小送風(fēng)策略，或噴口的布置高度盡量低于分層面，從而減少射流卷吸造成的對流熱轉(zhuǎn)移；對于柱狀下送風(fēng)系統(tǒng)，室內(nèi)空氣流動較弱，非空調(diào)區(qū)向空調(diào)區(qū)的對流熱轉(zhuǎn)移有限，則可以多利用屋頂排風(fēng)，及時排除非空調(diào)區(qū)積聚的熱量。

4  結(jié)論

       本文通過實驗和CFD數(shù)值模擬方法，研究了柱狀下送風(fēng)和側(cè)壁噴口送風(fēng)系統(tǒng)的大空間建筑熱環(huán)境和區(qū)域間換熱特性。根據(jù)縮尺實驗結(jié)果，證實了CFD模擬能夠準(zhǔn)確獲得室內(nèi)熱環(huán)境參數(shù)和負(fù)荷結(jié)果。基于相似理論，進(jìn)一步將縮尺工況拓展到全尺寸模擬研究，針對非空調(diào)區(qū)向空調(diào)區(qū)的熱量遷移，主要結(jié)論如下：

       對于柱狀下送風(fēng)系統(tǒng)，由于室內(nèi)氣流相對穩(wěn)定，湍流度較小，因此溫差引起的熱傳導(dǎo)占主導(dǎo)作用。而在側(cè)壁噴口送風(fēng)系統(tǒng)中，室內(nèi)空氣湍流度較大，溫差引起的熱傳導(dǎo)和氣流流動引起的換熱量均不容忽視。氣流的湍流脈動特性對區(qū)域間換熱存在主要影響，由于Cb取決于湍流粘性系數(shù)和空氣的湍流普朗特數(shù)，而噴口送風(fēng)系統(tǒng)的分界面處氣流擾動較強，因此側(cè)壁噴口送風(fēng)系統(tǒng)的區(qū)域間換熱系數(shù)遠(yuǎn)大于柱狀下送風(fēng)系統(tǒng)。Cb受送風(fēng)方式和區(qū)域劃分的影響，并與局部湍流強度有關(guān)。

參考文獻(xiàn)

       [1] 鄒月琴，王師白，彭榮等. 分層空調(diào)熱轉(zhuǎn)移負(fù)荷計算方法的研究[J]. 暖通空調(diào)，1983，13(3): 13-20.
       [2] 陸耀慶．實用供熱空調(diào)設(shè)計手冊第二版[M]. 中國建筑工業(yè)出版社，2008
       [3] Bing W, Li L, Gao Y, et al. Energy saving potentials of all cold air distribution system with stratified air conditioning in large space building[C]//Energy Sustainability. 2008, 43192: 261-266.
       [4] Togari S, Arai Y, Miura K, A simplified model for predicting vertical temperature distribution in a large space.  In: ASHRAE Trans, 1993, 99(1): 84-90.
       [5] Gao, J., Zhang, X., Zhao, J. N., & Gao, F. S. (2010). A heat transfer parameter at air interfaces in the block model for building thermal environment. International Journal of Thermal Sciences, 49(2), 463-470.
       [6] Chen Q. Ventilation performance prediction for buildings: A method overview and recent applications[J]. Building and environment, 2009, 44(4): 848-858.
       [7] 范存養(yǎng). 大空間建筑空調(diào)設(shè)計及工程實錄[M]. 中國建筑工業(yè)出版社, 2001.
       [8] Gebhart B. A new method for calculating radiant exchanges[J]. ASHRAE transactions, 1959, 65.

       備注：本文收錄于《建筑環(huán)境與能源》2021年4月刊 總第42期（第二十屆全國暖通空調(diào)模擬學(xué)術(shù)年會論文集）。版權(quán)歸論文作者所有，任何形式轉(zhuǎn)載請聯(lián)系作者。