天津大學(xué)  程思涵  田喆  吳霞

       【摘  要】服務(wù)業(yè)消耗能源比例日漸提高，服務(wù)部門(mén)的大部分能源用于辦公建筑取暖、照明、計(jì)算和餐飲。辦公用電又是辦公建筑能耗的重要組成部分，因此，建立高精度的電負(fù)荷曲線(xiàn)模型至關(guān)重要。本文利用馬爾科夫鏈蒙特卡洛方法，通過(guò)轉(zhuǎn)移概率矩陣建立人員模型，得到有效用電人數(shù)；結(jié)合統(tǒng)計(jì)調(diào)研數(shù)據(jù)，利用不同電器不同時(shí)刻不同功率的使用概率，建立了電器模型。結(jié)合人員模型和電器模型，通過(guò)自下而上的建模思想得到日負(fù)荷曲線(xiàn)分布。所建模型具有系統(tǒng)性和通用性，仿真與實(shí)測(cè)對(duì)比分析驗(yàn)證了本文模型的可行性與準(zhǔn)確性。

       【關(guān)鍵詞】自下而上，馬爾科夫鏈，蒙特卡洛，電負(fù)荷

0 引言

       近年來(lái)，我國(guó)經(jīng)濟(jì)水平飛速發(fā)展，建筑能耗水平也隨之不斷增長(zhǎng)，辦公建筑能耗作為我國(guó)建筑能耗的重要組成部分，其中電能占了很大比例。隨著社會(huì)經(jīng)濟(jì)發(fā)展，辦公用電仍有很大增長(zhǎng)空間^[1]。同時(shí)，辦公建筑日負(fù)荷曲線(xiàn)的獲取有利于推進(jìn)智能電網(wǎng)、需求響應(yīng)等技術(shù)的發(fā)展^[2,3]。因此辦公建筑日負(fù)荷曲線(xiàn)建模很有必要。

       目前，有兩種常用的電負(fù)荷曲線(xiàn)建模方法：一種是統(tǒng)計(jì)的方法，另一種是自下而上的方法。在統(tǒng)計(jì)方法中，研究對(duì)象是基于一組測(cè)量的負(fù)荷曲線(xiàn)，用其來(lái)描述輸入數(shù)據(jù)的特征，然后根據(jù)提取的特征制定負(fù)荷模型[4]；而在自下而上的方法中，終端電器是研究對(duì)象，重點(diǎn)是各個(gè)終端電器的使用模式制定，并以此得到總用電量^[5,6]。

       關(guān)于統(tǒng)計(jì)建模方法，文獻(xiàn)[7]采用時(shí)變多元回歸模型來(lái)進(jìn)行電負(fù)荷建模，作者考慮到用戶(hù)行為和公用事業(yè)生產(chǎn)效率變化，可以得到小時(shí)級(jí)的負(fù)荷曲線(xiàn)結(jié)果。王等人^[8]提出了一種分解方法，通過(guò)分解測(cè)量數(shù)據(jù)以提取不同時(shí)間尺度(如季節(jié)和工作日)模式，進(jìn)而模擬電力需求趨勢(shì)。斯蒂芬等人^[9]假設(shè)電力負(fù)荷服從非平穩(wěn)多元高斯分布，進(jìn)而提出了一個(gè)分析國(guó)內(nèi)能源客戶(hù)消費(fèi)習(xí)慣的框架。關(guān)于自下而上建模方法，Paatero和Lund^[10]根據(jù)季節(jié)和社會(huì)因素，將單個(gè)電器的啟動(dòng)建模為隨機(jī)過(guò)程，利用兩個(gè)主要數(shù)據(jù)集作為輸入構(gòu)建了一個(gè)兩級(jí)模型：第一級(jí)定義了為每個(gè)家庭設(shè)置的家用設(shè)備以及總體負(fù)荷波動(dòng)趨勢(shì)，第二級(jí)借助最終使用的啟動(dòng)概率來(lái)模擬每個(gè)家庭中的每個(gè)電器。Stoke在^[11]中提出了一個(gè)可以生成三種類(lèi)型聚合負(fù)荷曲線(xiàn)模型：第一層根據(jù)相關(guān)負(fù)荷和電器數(shù)據(jù)歸一化建模，得到普通家庭的30分鐘需求曲線(xiàn)，第二層考慮到家庭收入、生活方式等得到指定住宅的30分鐘需求曲線(xiàn)；第三層通過(guò)對(duì)啟動(dòng)概率建模來(lái)得到具有精細(xì)分辨率的選定家庭的1分鐘需求曲線(xiàn)。Capasso等人^[12]基于在意大利進(jìn)行的使用時(shí)間調(diào)查，建模了單個(gè)電器的開(kāi)始和持續(xù)時(shí)間，以及附加到每個(gè)電器的電力負(fù)載，通過(guò)匯總單個(gè)電器的消耗來(lái)建立住宅區(qū)的負(fù)荷曲線(xiàn)。Walker和Pokoski^[13]對(duì)這一模型進(jìn)行了改進(jìn)，其人行為建模的基礎(chǔ)是使用兩種概率函數(shù)，分別稱(chēng)為可用性函數(shù)和傾向性函數(shù)，然后將其推廣到Capasso等人的模型中。C. Sandels等人^[14]利用馬爾科夫鏈模擬辦公人員在室狀態(tài)，從而建立自下而上模型生成北歐具有代表性的辦公樓用電負(fù)荷曲線(xiàn)。

       從上述研究可以看出來(lái)，統(tǒng)計(jì)建模方法可以利用宏觀(guān)經(jīng)濟(jì)、能源價(jià)格和收入以及其他區(qū)域或國(guó)家指標(biāo)，更易于開(kāi)發(fā)和使用，還不需要詳細(xì)數(shù)據(jù)。但是這種方法并沒(méi)有提供太多細(xì)節(jié)和靈活性，從而導(dǎo)致精度不夠，而且需要大樣本。另外，統(tǒng)計(jì)建模方法通常難以解釋和調(diào)查用戶(hù)行為的影響。顯然，自下而上的方法雖然需要大量能夠反映家電消費(fèi)行為的數(shù)據(jù)，但預(yù)測(cè)精度很高。對(duì)于自下而上方法來(lái)說(shuō)，其模型主要存在三方面的不同：對(duì)成員行為描述的詳細(xì)程度、對(duì)影響電器負(fù)荷分布的電器數(shù)據(jù)描述詳細(xì)程度以及所使用的隨機(jī)方法。在現(xiàn)有的文獻(xiàn)研究中，很少有人既考慮到成員行為的隨機(jī)性又考慮到電器使用數(shù)據(jù)的隨機(jī)性。因此，本文綜合考慮到成員行為以及電器使用功率和概率情況，建立了基于馬爾科夫鏈蒙特卡洛方法的自下而上電負(fù)荷曲線(xiàn)模型。

       本文利用馬爾科夫鏈蒙特卡洛方法，通過(guò)轉(zhuǎn)移概率矩陣得到室內(nèi)有效用電人數(shù)，建立了人員模型；結(jié)合統(tǒng)計(jì)調(diào)研數(shù)據(jù)，利用不同電器不同時(shí)刻不同功率的使用概率，建立了電器模型。通過(guò)自下而上的建模思想結(jié)合人員模型和電器模型，得到日負(fù)荷曲線(xiàn)分布。所建模型具有系統(tǒng)性和通用性，適用于需求側(cè)管理以及智能電網(wǎng)研究。

1 辦公建筑日負(fù)荷建模體系

       對(duì)于辦公建筑的電負(fù)荷來(lái)說(shuō)，可以分為基礎(chǔ)負(fù)荷和與人員行為有關(guān)的負(fù)荷，基礎(chǔ)負(fù)荷即對(duì)應(yīng)電器功率保持固定值或者呈一定周期變化。對(duì)于與人員有關(guān)的負(fù)荷來(lái)說(shuō)，建筑內(nèi)人的行為會(huì)影響到對(duì)應(yīng)電器的使用情況，建筑內(nèi)人行為具有較大的隨機(jī)性，但是因?yàn)檗k公建筑內(nèi)部人員具有相對(duì)固定的作息時(shí)間，所以人員行為又具有一定的規(guī)律性，因此結(jié)合人員行為構(gòu)建辦公建筑日負(fù)荷曲線(xiàn)模型具有重要意義。

       本文的辦公建筑日負(fù)荷曲線(xiàn)建模體系如圖1所示，首先根據(jù)負(fù)荷特性將負(fù)荷分為與人員行為有關(guān)的負(fù)荷和基礎(chǔ)負(fù)荷，進(jìn)而找到對(duì)應(yīng)的電器。對(duì)于基礎(chǔ)電器來(lái)說(shuō)，某確定時(shí)刻的功率即為額定功率。對(duì)于與人有關(guān)的電器來(lái)說(shuō)，首先通過(guò)轉(zhuǎn)移概率矩陣建立人員模型，得到有效使用電器的人數(shù)；然后，根據(jù)統(tǒng)計(jì)調(diào)研數(shù)據(jù)，得到電器在不同時(shí)刻不同功率的使用概率，據(jù)此建立電器模型。根據(jù)人員模型和電器模型獲得單個(gè)電器的日負(fù)荷分布曲線(xiàn)，再疊加所有電器得到房間的日負(fù)荷曲線(xiàn)分布情況。

圖1 基于馬爾科夫鏈蒙特卡洛方法的自下而上辦公建筑日負(fù)荷曲線(xiàn)建模體系

2 辦公負(fù)荷人員模型

       電器的使用情況并不是完全隨機(jī)的，很大程度受到室內(nèi)人員的影響。本文基于英國(guó)TUS（Time-Use Survey）數(shù)據(jù)庫(kù)^[15]，利用馬爾科夫鏈蒙特卡洛方法來(lái)生成有效用電人數(shù)。英國(guó)TUS 數(shù)據(jù)庫(kù)對(duì)大量辦公建筑進(jìn)行調(diào)研，以15min為統(tǒng)計(jì)精度， 記錄1天24 h活動(dòng)日程，可以由此統(tǒng)計(jì)出1天內(nèi)各時(shí)刻參與者的活動(dòng)位置，得到建筑內(nèi)的人員數(shù)量及其從事各種活動(dòng)的概率。

       2.1 MCMC方法

       MCMC方法是一種特殊的蒙特卡洛方法，其將隨機(jī)過(guò)程中的馬爾科夫鏈應(yīng)用于蒙特卡洛模擬中，抽樣分布隨模擬的進(jìn)行而改變，從而實(shí)現(xiàn)動(dòng)態(tài)模擬。

       馬爾科夫過(guò)程基于如下的思想：若隨機(jī)過(guò)程在時(shí)刻t_i 的狀態(tài)已知，且在時(shí)刻t>t_i 的狀態(tài)僅與時(shí)刻t_i的狀態(tài)有關(guān)，而與t_i前的狀態(tài)無(wú)關(guān)，這個(gè)特性稱(chēng)為馬爾科夫性或無(wú)后效性^[16]。馬爾科夫鏈模型基于狀態(tài)轉(zhuǎn)移矩陣( 即從某一狀態(tài)轉(zhuǎn)移到另一狀態(tài)的概率) 建立，其中一階馬爾科夫鏈表示一個(gè)隨機(jī)序列的條件概率只與前一時(shí)刻的系統(tǒng)狀態(tài)有關(guān)， 而與之前的系統(tǒng)狀態(tài)無(wú)關(guān)。其狀態(tài)轉(zhuǎn)移概率矩陣 P 如下所示：

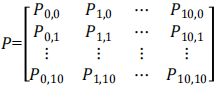                           （1）

       2.2 有效用電人數(shù)

       建筑內(nèi)電器的使用與有效用電人數(shù)密切相關(guān)，有效用電人數(shù)指的是某一時(shí)刻正在使用電器的人數(shù)。基于TUS數(shù)據(jù)庫(kù)，每15分鐘建立一個(gè)狀態(tài)轉(zhuǎn)移矩陣，考慮到某些房間可能人數(shù)較多，故房間人數(shù)分區(qū)間設(shè)置，分別為總?cè)藬?shù)的10%，20%...100%。利用MCMC方法仿真各時(shí)刻的有效人數(shù)nt如下公式：

       n_t=f(n,P_i,j,t)          （2）

       其中的n為總?cè)藬?shù)，P_i,j為轉(zhuǎn)移概率，公式如下：

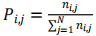                  （3）

       它表示由狀態(tài)i轉(zhuǎn)移到狀態(tài)j的次數(shù)除以狀態(tài)i的總轉(zhuǎn)移次數(shù)，比如P_1,2表示上一時(shí)刻的有效人數(shù)占比為0.1轉(zhuǎn)移到下一時(shí)刻有效人數(shù)占比為0.2的概率。各時(shí)刻室內(nèi)有效人數(shù)仿真流程如下圖2：

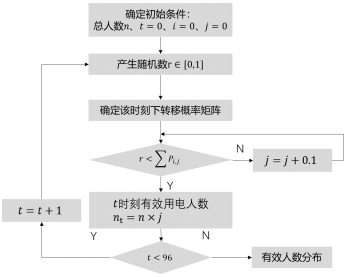
圖2 有效人數(shù)生成的算法流程

       （1）確定總?cè)藬?shù)n，初始時(shí)刻設(shè)置為0，初始狀態(tài)設(shè)置為有效人數(shù)占比0；

       （2）基于統(tǒng)計(jì)數(shù)據(jù)，利用MCMC方法，將生成的隨機(jī)數(shù)與不同時(shí)刻轉(zhuǎn)移概率矩陣的累計(jì)概率比較，確定不同時(shí)刻的有效人數(shù)；

       （3）循環(huán)96次，得到有效人數(shù)在一天內(nèi)的分布情況。

3 電器模型

       由前述可知，辦公建筑內(nèi)的電器可以分為基礎(chǔ)電器和與人有關(guān)的電器。基礎(chǔ)電器的瞬時(shí)功率即為當(dāng)前時(shí)刻的額定功率，計(jì)算公式如下：

       P_b,T=P_e,T                  （3）

       其中P_e,T為T(mén)時(shí)刻該電器的額定功率。

       接下來(lái)主要講述如何確定與人有關(guān)電器的瞬時(shí)功率值，計(jì)算流程如下圖3所示：

圖3 與人有關(guān)電器的瞬時(shí)功率值計(jì)算流程

       （1）根據(jù)統(tǒng)計(jì)數(shù)據(jù)，得到不同電器不同時(shí)間不同功率的使用概率，這里將設(shè)備的功率值按照實(shí)際情況分為不同的檔數(shù)，假設(shè)為k檔。

       （2）利用隨機(jī)數(shù)與累計(jì)概率比較，確定單臺(tái)某電器在T時(shí)刻的功率如下公式：

                       （4）

       其中L^m_k代表電器m在第k檔的功率值，β為隨機(jī)數(shù)，p_T,i表示T時(shí)刻不同檔位功率的概率。

       （3）結(jié)合人員模型確定的有效用電人數(shù)，再引入共用系數(shù)α，得到T時(shí)刻某設(shè)備的功率如下公式：

        P_m,T=Σ^ant_i=1P_m,s,i                  （5）

       其中，n_t為有效人數(shù)，i為進(jìn)行蒙特卡洛抽取的次數(shù)，α為共用系數(shù)，反應(yīng)電器共用情況，公式如下：

                                      （6）

       其中A為同時(shí)使用人數(shù)。

       （4）將這一過(guò)程循環(huán)M次就可以得到與人有關(guān)的設(shè)備總功率的瞬時(shí)值，公式如下：

       P_p,T=Σ^M_m=1P_m,T          （7）

       其中M表示設(shè)備種類(lèi)。

4、辦公建筑日負(fù)荷曲線(xiàn)仿真

       辦公建筑的負(fù)荷特征由建筑內(nèi)人員行為和開(kāi)啟的電器共同決定，結(jié)合人員模型和電器模型可以得到辦公建筑日負(fù)荷曲線(xiàn)。

       4.1 仿真結(jié)構(gòu)

       辦公建筑日負(fù)荷曲線(xiàn)仿真結(jié)構(gòu)如圖4所示。結(jié)合人員模型和電器模型可以得到單個(gè)電器功率分布，進(jìn)而得到所有與人有關(guān)的電器功率分布，再加上基礎(chǔ)電器，將各時(shí)刻所有電器負(fù)荷曲線(xiàn)疊加即可獲得日負(fù)荷曲線(xiàn)，日負(fù)荷瞬時(shí)值如下公式：

       P_T=P_b,T+P_p,T                 （8）

       其中P_b,T為基礎(chǔ)電器瞬時(shí)功率，P_b,T為與人有關(guān)電器瞬時(shí)功率。

圖4 辦公建筑日負(fù)荷曲線(xiàn)仿真結(jié)構(gòu)圖

       4.2 模型校驗(yàn)

       4.2.1 案例介紹與模型數(shù)據(jù)來(lái)源

       為了驗(yàn)證該辦公建筑日負(fù)荷曲線(xiàn)模型的有效性，選取某行政辦公樓的某一房間進(jìn)行校驗(yàn)。該辦公室共有35人，電器擁有情況為飲水機(jī)1臺(tái)，空氣凈化器1臺(tái)，電腦35臺(tái)，燈12個(gè)，打印機(jī)3臺(tái)。作息時(shí)間為9:00-17:00，周末休息。具體電器情況見(jiàn)下表1：

表1 辦公室內(nèi)電器情況

       通過(guò)調(diào)研得知，打印機(jī)的工作功率為360W，不工作時(shí)的待機(jī)功率為10W；12盞燈采用“一開(kāi)全開(kāi)，一關(guān)全關(guān)”的狀態(tài)，打開(kāi)時(shí)功率為48W，關(guān)閉時(shí)為0，所以對(duì)于打印機(jī)和燈來(lái)說(shuō)均為兩檔功率。對(duì)于電腦來(lái)說(shuō)，通過(guò)實(shí)際調(diào)研發(fā)現(xiàn)其功率分布在0-150W之間，故每10W設(shè)置為一檔位。對(duì)辦公室內(nèi)的電器進(jìn)行為期一周的實(shí)際使用情況監(jiān)測(cè)，每天每15分鐘記錄一次使用情況，從而得到不同電器不同時(shí)間段的使用情況。由于該辦公樓為行政辦公樓，加班情況較少但是也不排除，故結(jié)合國(guó)家統(tǒng)計(jì)局的相關(guān)數(shù)據(jù)資料，將非工作時(shí)間的電器使用概率均假設(shè)為0.05。由此，辦公室內(nèi)電器不同時(shí)刻不同功率的使用概率如下圖5-7。

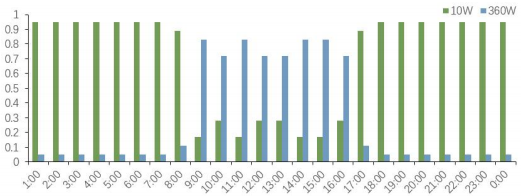
圖5 打印機(jī)不同時(shí)刻不同功率使用概率

圖6 燈不同時(shí)刻不同功率使用概率

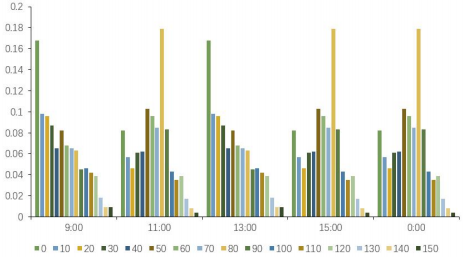
圖7  電腦不同時(shí)刻不同功率使用概率

       4.2.2 仿真結(jié)果與分析

       根據(jù)前述辦公室的信息，利用MCMC方法，得到的有效人數(shù)分布情況如下圖8，從有效人數(shù)分布來(lái)看，上下午各有一個(gè)峰值，午休時(shí)間會(huì)有一個(gè)谷值，這是由于辦公建筑的固定工作時(shí)間造成的，工作時(shí)間之外還考慮到一定的加班情況，故也有較少人數(shù)分布。

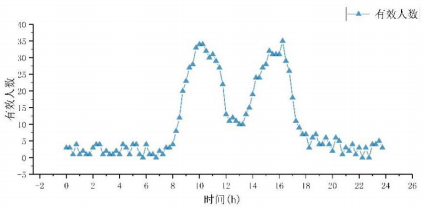
圖8 有效人數(shù)分布情況

       平均日負(fù)荷曲線(xiàn)通常用來(lái)作為選擇配電系統(tǒng)元件容量的標(biāo)準(zhǔn)。故將一周5天工作日的模型數(shù)據(jù)與實(shí)測(cè)數(shù)據(jù)平均值作對(duì)比，以驗(yàn)證所建模型的有效性。圖9是該辦公室一周5個(gè)工作日的功率均值對(duì)比情況。由圖9看出，模型結(jié)果與實(shí)測(cè)數(shù)據(jù)具有較好的相似性。

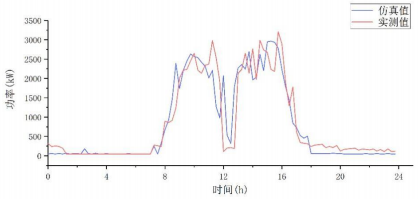
圖9 該辦公室日負(fù)荷均值仿真值與實(shí)測(cè)值對(duì)比

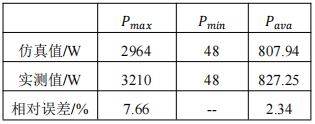
       將5天內(nèi)模型數(shù)據(jù)與實(shí)測(cè)數(shù)據(jù)的最大值、最小值及平均值作對(duì)比，以驗(yàn)證所建模型的有效性。如下表2所示，因?yàn)橛幸欢ǖ幕A(chǔ)負(fù)荷晝夜保持運(yùn)行，故最小值一致，對(duì)于最大值和平均值來(lái)說(shuō)，最大相對(duì)誤差為7.66%，在可接受范圍內(nèi)，仿真值與實(shí)測(cè)值具有較高一致性，故模型較為準(zhǔn)確。

表2 電負(fù)荷最大值，最小值以及平均值的仿真值和實(shí)測(cè)值對(duì)比

       該辦公室一周5天工作日的概率密度曲線(xiàn)如圖10所示。可以看出，實(shí)測(cè)值與仿真值的概率密度曲線(xiàn)具有良好的一致性。

圖10 該辦公室功率概率密度曲線(xiàn)仿真值與實(shí)測(cè)值對(duì)比

5 結(jié)論

       本文基于統(tǒng)計(jì)調(diào)研數(shù)據(jù)，利用馬爾科夫鏈蒙特卡洛方法建立了自下而上的辦公建筑日負(fù)荷曲線(xiàn)模型。利用馬爾科夫鏈蒙特卡洛方法建立人員模型得到有效使用電器人數(shù)；利用統(tǒng)計(jì)調(diào)研數(shù)據(jù)，確定不同電器不同時(shí)間不同功率的使用概率，據(jù)此建立電器模型。結(jié)合人員模型和電器模型得到日負(fù)荷分布情況。仿真與實(shí)測(cè)結(jié)果具有良好一致性，證實(shí)模型有效。該模型可以應(yīng)用于需求側(cè)管理、智能電網(wǎng)以及配電網(wǎng)動(dòng)態(tài)研究，具有重要工程價(jià)值。

參考文獻(xiàn)

       [1] 王葵, 李建超, 潘貞存,等. 居民用戶(hù)諧波調(diào)查及仿真分析[J]. 電力系統(tǒng)保護(hù)與控制, 2008(22):88-92.
       [2] 黃海新, 鄧麗, 文峰,等. 基于實(shí)時(shí)電價(jià)的用戶(hù)用電響應(yīng)行為研究[J]. 電力建設(shè), 2016, 37(2):63-68.
       [3] 朱海明. 電動(dòng)汽車(chē)充電模式對(duì)主動(dòng)配電網(wǎng)的影響[J]. 大科技, 2015, 36(028):97-102.
       [4] Hoverstad, B.A.；Tidemann, A.；Langseth, H. Short-term load forecasting with seasonal decomposition using evolution for parameter tuning[J]. IEEE Trans. Smart Grid 2015(6):1904–1913.
       [5] Chuan L ，Ukil A . Modeling and Validation of Electrical Load Profiling in Residential Buildings in Singapore[J]. IEEE Transactions on Power Systems, 2015, 30(5):2800-2809. 
       [6] Swan L G , Ugursal V I . Modeling of end-use energy consumption in the residential sector: A review of modeling techniques[J]. Renewable & Sustainable Energy Reviews, 2009, 13(8):1819-1835.
       [7] Dordonnat V , Koopman S J , Ooms M , et al. An Hourly Periodic State Space Model for Modelling French National Electricity Load[J]. Tinbergen Institute Discussion Papers, 2008.
       [8] [ Chi-hsiang Wang, Grozev G , Seo] S . Decomposition and statistical analysis for regional electricity demand forecasting[J]. Energy, 2012.
       [9] Stephen B , Mutanen A J , Galloway S , et al. Enhanced Load Profiling for Residential Network Customers[J]. IEEE Transactions on Power Delivery, 2014, 29(1):88-96.
       [10] Paatero J V , Lund P D . A model for generating household electricity load profiles[J]. International Journal of Energy Research, 2010, 30(5):273-290.
       [11] Stokes M . Removing barriers to embedded generation : a fine-grained load model to support low voltage network performance analysis[J]. De Montfort University, 2005.
       [12] Capasso A , Grattieri W . A bottom-up approach to residential load modeling[J]. IEEE Transactions on Power Systems, 1994, 9(2):957-964.
       [13] Walker C F , Pokoski J L . Residential Load Shape Modeling Based on Customer Behavior[J]. IEEE Power Engineering Review, 1985, PER-5(7):34-34.
       [14] Sandels C , Brodén, D, Widén, J, et al. Modeling office building consumer load with a combined physical and behavioral approach: Simulation and validation[J]. APPLIED ENERGY -BARKING THEN OXFORD-, 2016, 162:472-485.
       [15] Milanovic J V , Yamashita K , Martinez Villanueva S , et al. International Industry Practice on Power System Load Modeling[J]. IEEE TRANSACTIONS ON POWER SYSTEMS PWRS, 2013, 28(3):3038-3046.
       [16] Nijhuis M , Gibescu M , Cobben J F G . Bottom-up Markov Chain Monte Carlo approach for scenario based residential load modelling with publicly available data[J]. Energy & Buildings, 2016, 112.

       備注：本文收錄于《建筑環(huán)境與能源》2021年4月刊 總第42期（第二十屆全國(guó)暖通空調(diào)模擬學(xué)術(shù)年會(huì)論文集）。版權(quán)歸論文作者所有，任何形式轉(zhuǎn)載請(qǐng)聯(lián)系作者。